Lors de l’élaboration de prévisions financières, toute entreprise doit poser des hypothèses. Dans certains cas, les hypothèses seront plus simples à formuler, dans d’autres cas, elles seront plus complexes. De même, certaines hypothèses auront peu d’impact sur les résultats de l’entreprise et d’autres auront un impact monumental. Dans tous les cas, vous souhaiterez utiliser un modèle financier capable de prévoir les résultats de divers scénarios. Mieux encore, vous pourriez avoir recours à une approche qui vous permettra de prévoir avec plus de certitude vos hypothèses: l’approche Monte-Carlo.
Pourquoi vous devriez vous intéresser à l’approche Monte-Carlo?
L’usage de l’approche Monte-Carlo dans le cadre de l’élaboration de prévisions financières va vous permettre de réduire considérablement l’incertitude entourant vos hypothèses et de mesurer plus précisément le risque rattaché à certaines des variables de votre modèle d’affaires. Ainsi, vous gagnerez confiance en vos prévisions et vous maîtriserez mieux les éléments d’incertitude de votre entreprise.
Comment fonctionne l’approche Monte-Carlo?
Le terme méthode de Monte-Carlo, ou méthode Monte-Carlo, désigne toute méthode visant à calculer une valeur numérique en utilisant des procédés aléatoires, c’est-à-dire des techniques probabilistes.
La méthode de simulation de Monte-Carlo permet aussi d’introduire une approche statistique du risque dans une décision financière. Elle consiste à isoler un certain nombre de variables-clés du projet, tels que le chiffre d’affaires ou la marge, et à leur affecter une distribution de probabilités. Pour chacun de ces facteurs, un grand nombre de tirages aléatoires est effectué dans les distributions de probabilité déterminées précédemment, afin de trouver la probabilité d’occurrence de chacun des résultats.
Wikipedia
Les distributions de probabilités les plus fréquentes
La distribution la plus utilisée et la plus connue est sans aucun doute la “Loi normale”. C’est la courbe en forme de cloche (tel qu’illustré à l’image suivante). Dans ce type de distribution, on doit connaître la moyenne et la valeur approximative de l’écart-type. C’est ce qui permettra de distribuer les résultats autour de la moyenne. Dans cette forme de distribution, les probabilités de se retrouver autour de la moyenne sont plus élevées que de s’y éloigner.
Parmi les autres formes de distributions de probabilités, on retrouve notamment:
- La loi normale logarithmique (la “log-normale”)
- La loi uniforme et uniforme continue
- La loi triangulaire
- La loi discrète
- Etc.
Si vous avez bien compris les explications, vous saisissez que pour utiliser efficacement l’approche Monte-Carlo, l’entreprise doit avoir une bonne compréhension du type de distribution de ses données clés.
Vous devez évaluer une entreprise, analyser un projet d’investissement et/ou analyser les états financiers d’une entreprise ? Maîtrisez les grands concepts et méthodes de calcul appropriées avec nos formations en finance corporative. |
|---|
Un exemple d’analyse Monte-Carlo
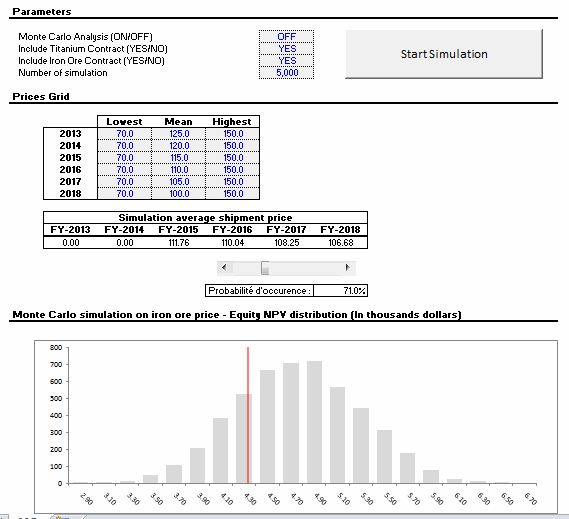
Dans l’exemple ci-dessous, on a utilisé l’approche Monte-Carlo pour déterminer la “NPV” (Net Present Value) ou en français la “VAN” (Valeur actuelle nette), en fonction de la distribution potentielle du prix du fer au cours des 6 prochaines années. L’axe des X est composé de la valeur des “NPV” possibles. Les valeurs sur l’axe des Y représentent le nombre d’occurrences potentielles des “NPV” se trouvant sur l’axe des X. De plus, on a inséré un gadget qui nous permet de faire varier les % d’occurrences et ainsi observer les “NPV” correspondantes. Par exemple, dans l’image ci-bas, vous pouvez observer que dans 71% des cas, la “NPV” se trouve au-delà de la barre rouge, donc est supérieure à 4,30M$.
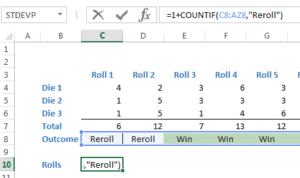
Vous noterez également que ces résultats ont été obtenus en produisant 5,000 simulations, dont voici un très court extrait.
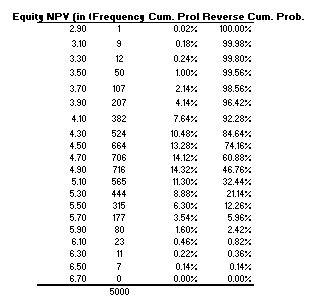
Une fois les 5,000 simulations terminées et compilées, l’analyse des valeurs de “NPV” ressemble à ce qui se trouve sur l’image ci-bas et c’est ce qui permet de faire le graphique de distribution.
Autre exemple illustré pas à pas
Nous avons publié 2 articles pour vous permettre d’apprendre à créer des simulations Monte-Carlo dans Excel, sans l’entremise du VBA. L’un de ces articles est un enregistrement d’un webinaire et l’autre un tutoriel pas à pas.
Formation complémentaire
Afin d’approfondir vos connaissances avec les simulations Monte-Carlo, nous vous recommandons notre formation Excel – Analyse de projets d’investissement.
Voici quelques commentaires d’apprenants ayant suivi cette formation :
La mission du CFO masqué est de développer les compétences techniques des analystes et des contrôleurs de gestion en informatique décisionnelle avec Excel et Power BI et favoriser l’atteinte de leur plein potentiel, en stimulant leur autonomie, leur curiosité, leur raisonnement logique, leur esprit critique et leur créativité.
ok