Maîtriser la régression linéaire dans Excel : un levier stratégique pour les décideurs

Dans un environnement d’affaires où les données abondent, savoir les interpréter efficacement devient un avantage concurrentiel. La régression linéaire, qui, pour plusieurs est un concept abstrait, étudié à l’école secondaire ou au CEGEP et vite oublié, est en réalité un outil puissant pour les gestionnaires, analystes et décideurs. Grâce à Excel, elle devient accessible et opérationnelle, même sans expertise statistique avancée.

Qu’est-ce que la régression linéaire?

La régression linéaire est une méthode statistique qui permet de modéliser la relation entre une variable dépendante (Y) et une ou plusieurs variables indépendantes (X).

Comme son nom l’indique, la régression linéaire repose sur l’hypothèse suivante : La relation entre la variable dépendante Y et la ou les variables explicatives X est linéaire, c’est-à-dire que les variations de Y peuvent être expliquées par une droite en fonction de X.

Cependant, toutes les relations ne sont pas linéaires. Certaines suivent des courbes ou des trajectoires plus complexes. Par exemple, les ventes d’un nouveau produit peuvent être très fortes au lancement, puis décroître par la suite (effet de nouveauté). À l’inverse, elles peuvent commencer modestement et croître rapidement par la suite (effet « hockey stick »).

Dans de tels cas, il faudra se tourner vers d’autres méthodes statistiques pour modéliser la relation entre les variables.

Comment savoir si nous sommes en présence d’une relation qui est linéaire ?

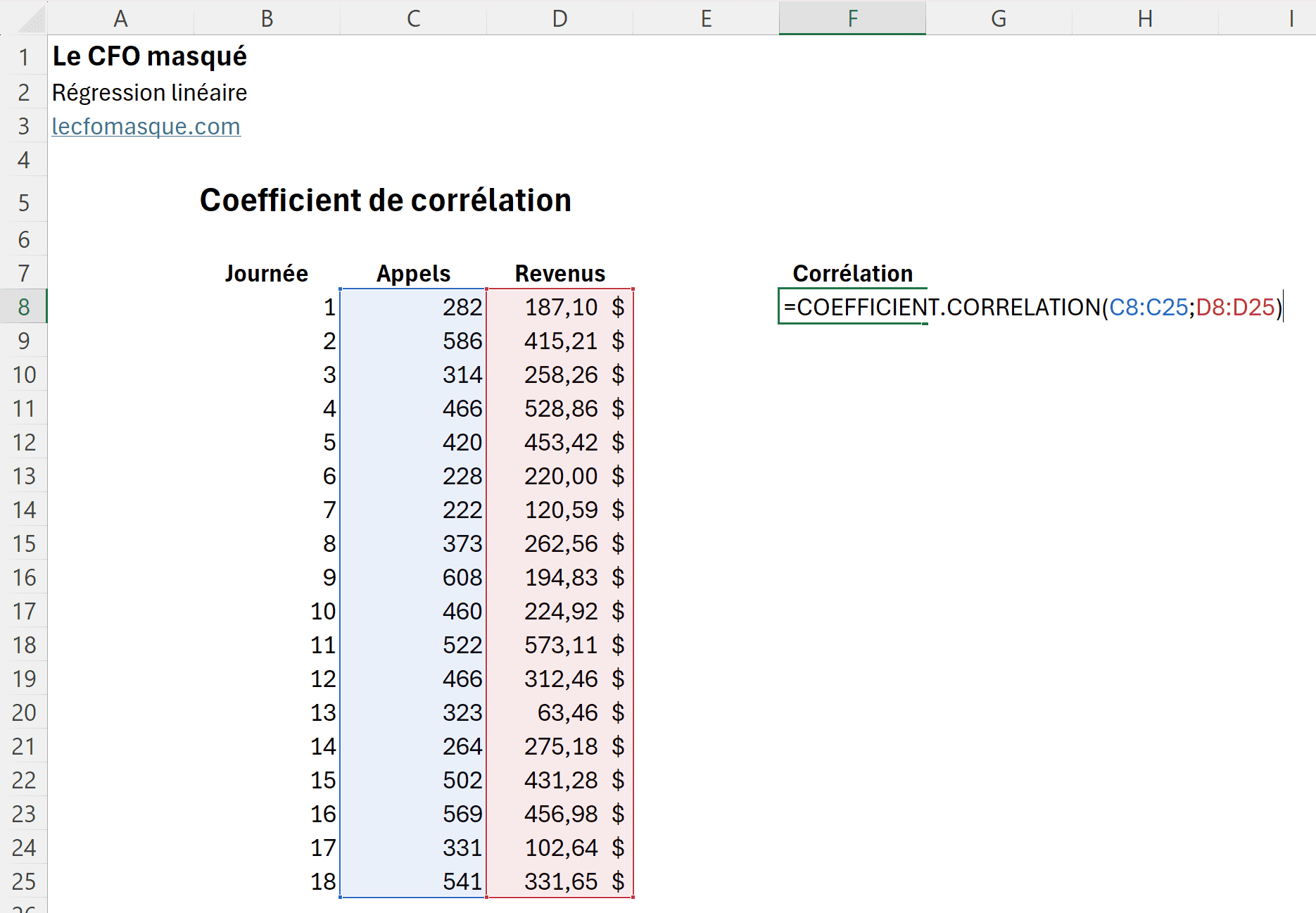
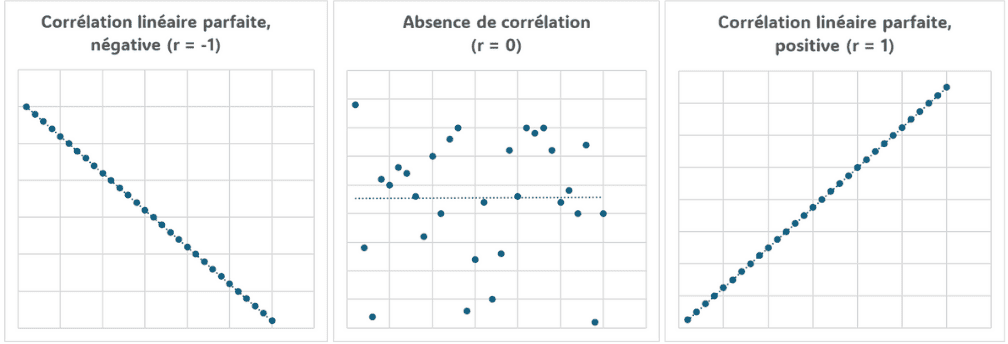
La première étape consiste à calculer le coefficient de corrélation r, qui varie entre -1 et 1.

r=0 : aucune corrélation linéaire.
r proche de 1 ou -1 : forte corrélation linéaire.

Dans Excel, la fonction suivante vous permet de calculer facilement le coefficient de corrélation entre deux variables :

=COEFFICIENT.CORRELATION(plage1; plage2)

Ce coefficient vous informe non seulement de la présence d’une relation linéaire, mais aussi sur :

• Le sens de la relation :
  • Positive : les variables évoluent dans le même sens.
  • Négative : elles évoluent en sens inverse.

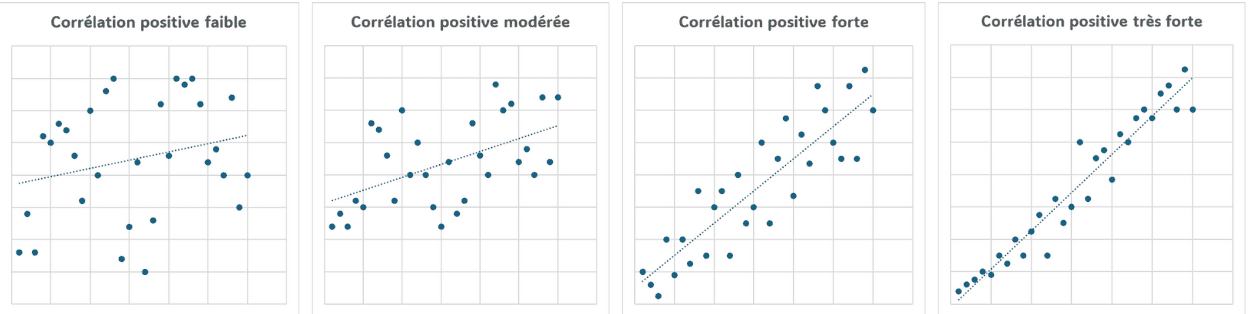
• La force de la relation :
  • Faible : r = 0 à ±0.3
  • Modérée : r = ±0.3 à ±0.6
  • Forte : r = ±0.6 à ±0.9
  • Très forte : r = ±0.9 à ±1

Attention : corrélation ≠ causalité

Un autre élément important à mentionner, parce qu’il s’agit d’une erreur fréquente : corrélation ne signifie pas causalité. Il est essentiel de considérer les autres facteurs pouvant influencer les résultats. En effet, pour reprendre un exemple courant, s’il existe une corrélation entre le nombre d’armes à feu dans une région et son taux de criminalité, peut-on conclure que le taux de criminalité est plus élevé car le nombre d’armes à feu est plus élevé ou alors que le nombre d’armes à feu est plus élevé car les gens souhaitent davantage se protéger dans les régions où la criminalité est plus importante ? Il ne faut pas oublier non plus que d’autres paramètres pourraient entrer en ligne de compte comme l’âge des personnes, leur niveau de revenu, leur niveau d’éducation, etc.

Exemple

Comme gestionnaire d’entreprise, je pourrais m’interroger sur la relation entre le nombre d’appels effectués par mon équipe de développement des affaires et le niveau de revenus générés. Pour ce faire, il suffirait de calculer le coefficient de corrélation entre le nombre d’appels effectués par jour et les ventes réalisées. Ci-bas, nous pouvons constater qu’il existe une relation positive entre ces deux variables. En effet, plus l’équipe de développement des affaires effectue d’appels téléphoniques, plus les ventes augmentent. Toutefois, cette corrélation, à 0.59, peut être qualifiée de modérée.

Vous aimeriez être un Ninja Excel et devenir la référence ultime de votre bureau, ou tout le moins ne plus avoir l’impression de stagner ? Développez des solutions innovatrices en explorant des fonctions et fonctionnalités souvent méconnues mais fort utiles avec nos formations pour devenir Ninja d’Excel.

Aller plus loin : la régression pour effectuer des prévisions

Pour réaliser une analyse de régression, qu’elle soit simple ou multiple, plusieurs méthodes sont possibles. Quelle que soit la méthode utilisée, l’objectif est de déterminer l’équation de la droite de régression afin de pouvoir estimer la valeur de Y en fonction des variables explicatives X.

La première méthode consiste à utiliser la fonction DROITEREG, qui permet de calculer directement les coefficients de la régression à partir des données sélectionnées. Cette fonction renvoie la pente associée à chaque variable indépendante, l’interception, ainsi que diverses statistiques telles que le coefficient de détermination (R²), les erreurs standards et la statistique F, selon les arguments utilisés. Elle s’effectue à l’aide d’une formule matricielle et ne nécessite pas d’outil complémentaire.

Pour en savoir plus sur comment mettre en pratique cette méthode, consultez notre article de blogue Analyse prédictive : Réaliser une régression linéaire simple avec la fonction DROITEREG dans Excel.

La deuxième méthode consiste à utiliser le Data Analysis Toolpak d’Excel, qui propose un module d’analyse de régression accessible via le menu Données > Analyse des données. Cet outil offre une interface conviviale permettant de sélectionner facilement la variable dépendante et les variables indépendantes, et il génère automatiquement un rapport détaillé comprenant les coefficients, le R², les statistiques de test, les intervalles de confiance et les valeurs prédites. C’est une méthode pratique pour obtenir une analyse complète sans avoir à manipuler de formules.

Pour en savoir plus sur comment mettre en pratique cette méthode, consultez notre article de blogue Analyse prédictive : Réaliser une régression linéaire multiple avec le Data Analysis Toolpak d’Excel.

Formation complémentaire

Développez vos compétences en analyse de données et exploitez les fonctions d’Excel qui permettent de manipuler, gérer et transformer des données qui proviennent de diverses sources et différents formats, sans faire intervenir Power Query ou le VBA, en suivant la formation Excel – Traitement, manipulation et analyse de données.

Voici quelques commentaires d’apprenants ayant suivi cette formation :

La mission du CFO masqué est de développer les compétences techniques des analystes et des contrôleurs de gestion en informatique décisionnelle avec Excel et Power BI et favoriser l’atteinte de leur plein potentiel, en stimulant leur autonomie, leur curiosité, leur raisonnement logique, leur esprit critique et leur créativité.