Dans cet article, nous verrons pas à pas comment réaliser une régression linéaire multiple dans Excel à l’aide du Data Analysis Toolpak. Cette méthode est particulièrement utile pour modéliser la relation entre plusieurs variables indépendantes (X1, X2, X3, …) et une variable dépendante (Y). Elle est sert à:
- Comprendre l’impact combiné de plusieurs facteurs.
- Identifier les variables les plus significatives.
- Améliorer la précision des prévisions.
Avant de débuter votre lecture, si ce n’est pas déjà fait, prenez le temps de bien comprendre les principes de base de la régression linéaire : qu’est-ce qu’une relation linéaire, comment la reconnaître, l’interpréter et éviter les principaux pièges. Vous pouvez approfondir ces notions en consultant notre article Maîtriser la régression linéaire dans Excel : un levier stratégique pour les décideurs.
Nous vous recommandons également de lire notre article sur la régression linéaire simple dans Excel, dans lequel nous expliquons comment utiliser la fonction DROITEREG (ou LINEST en anglais) pour modéliser la relation entre deux variables.
Le présent article va plus loin en abordant la régression linéaire multiple, où plusieurs variables indépendantes sont utilisées pour expliquer la variable dépendante.
1. Activer le Data Analysis Toolpak d’Excel
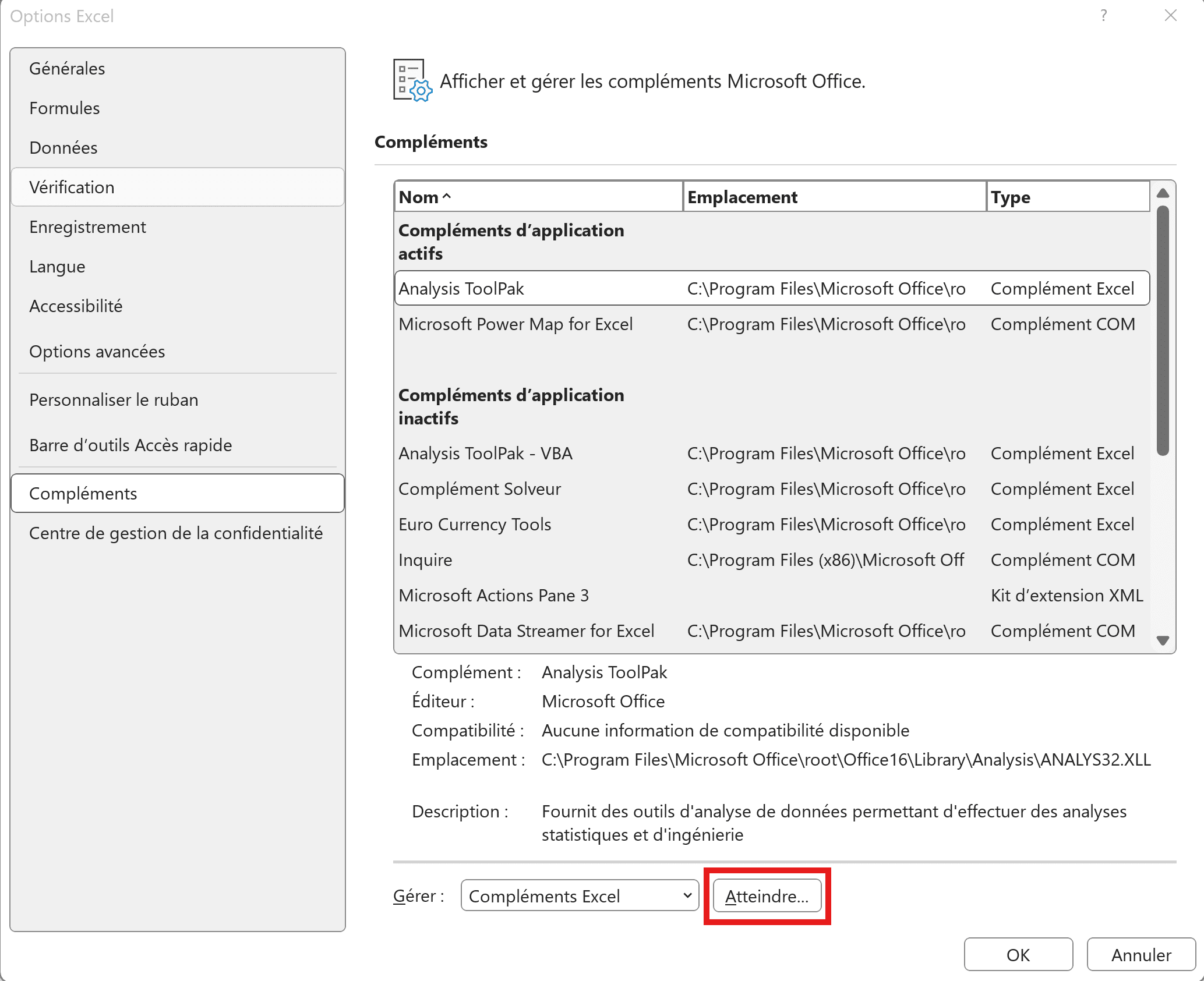
Tout d’abord, vous devez vous rendre dans Fichier : Options : Compléments, puis sélectionner Complément Excel dans le menu déroulant qui se trouvera dans le bas de la fenêtre. Cliquez ensuite sur Atteindre.
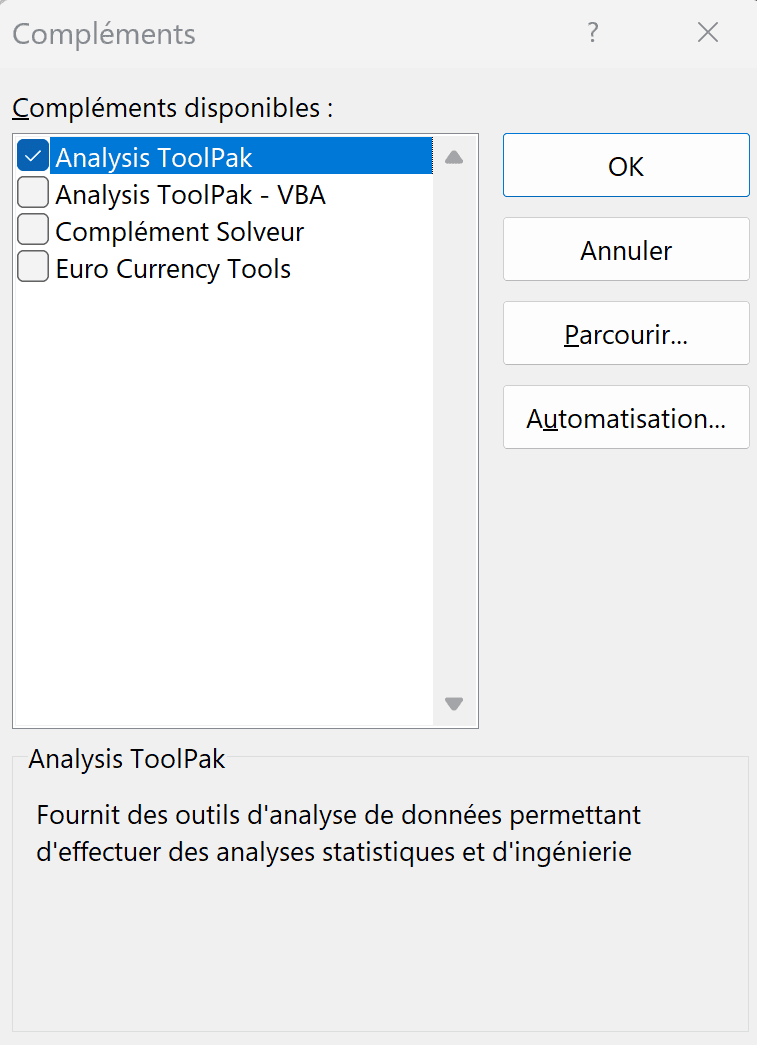
Cochez l’option Analysis TookPak, puis cliquez sur OK.
Vous remarquerez alors qu’un élément de navigation nommé Data Analysis se sera ajouté dans le menu Données de votre ruban Excel.
2. Préparer vos données
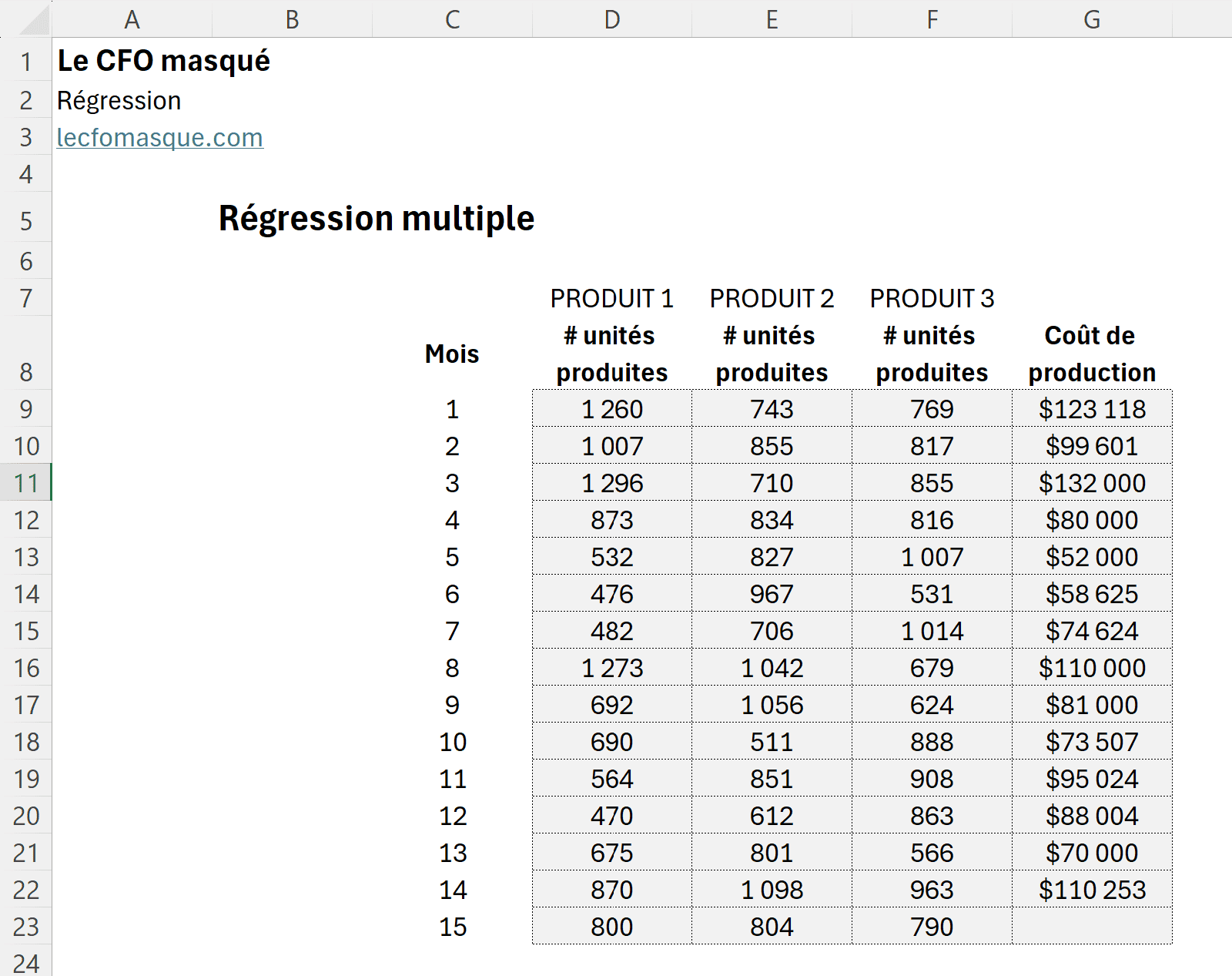
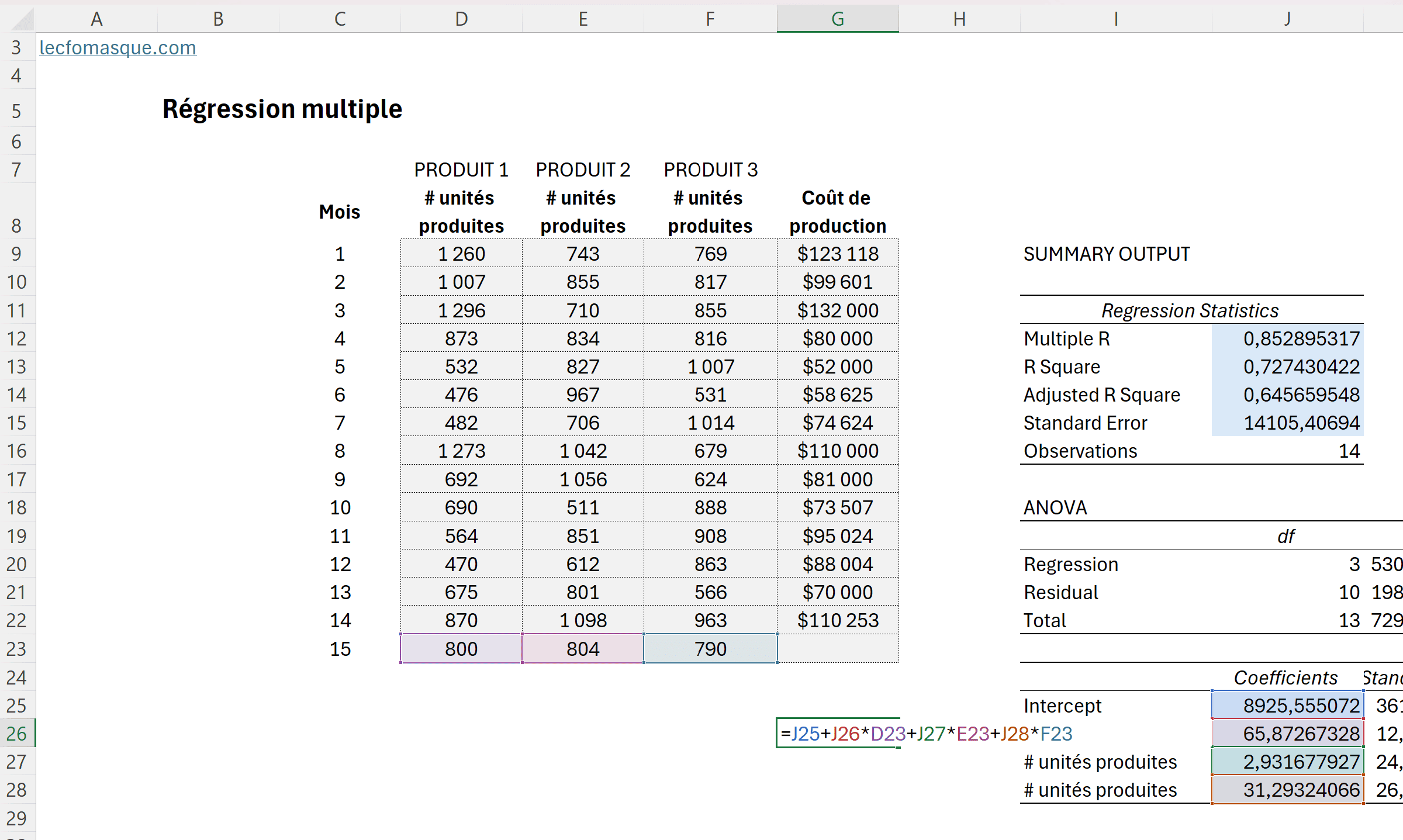
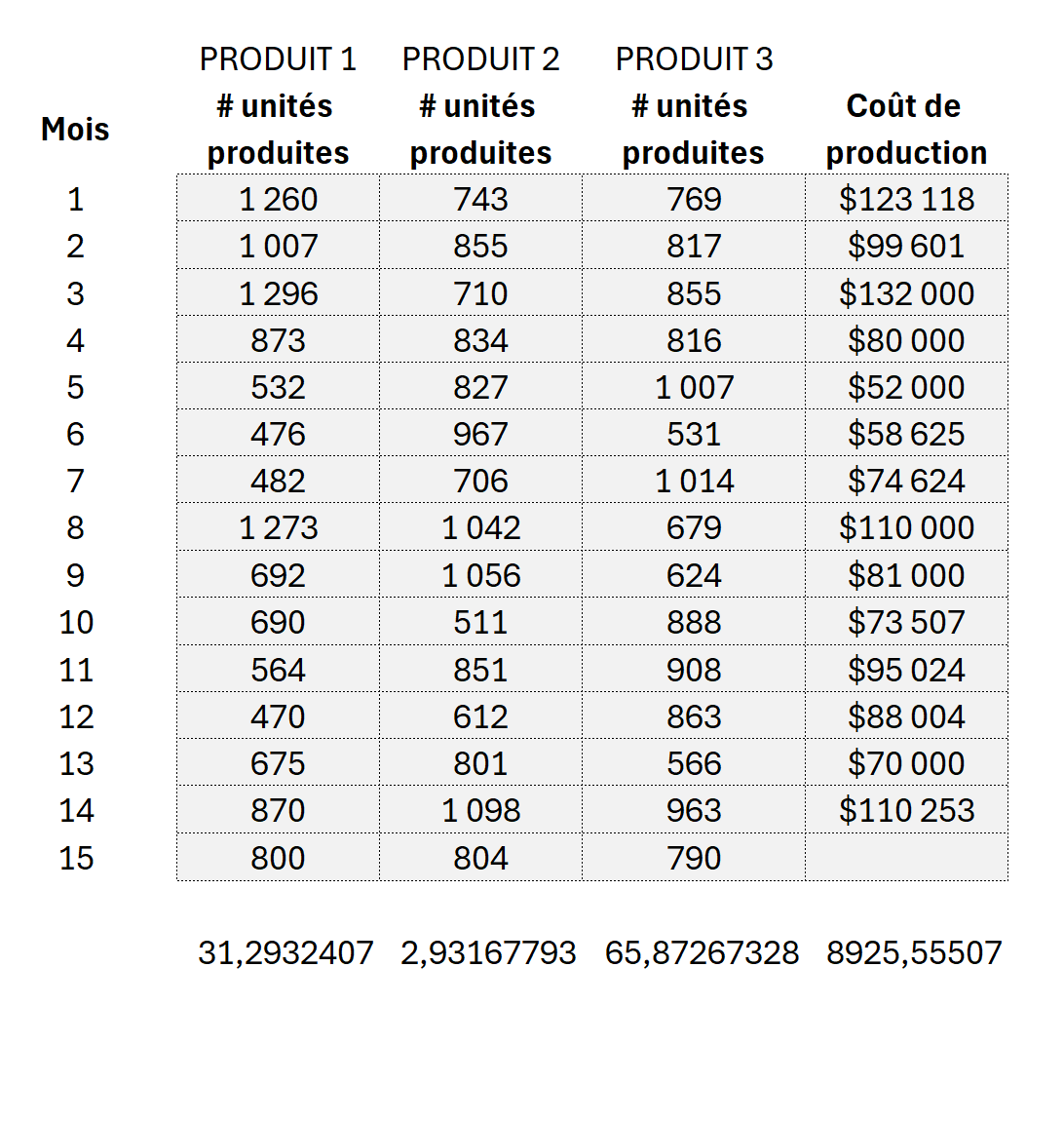
Dans notre exemple de régression linéaire multiple, nous avons les unités produites pour 3 produits différents et le coût de production total pour une certaine période d’observations.
3. Effectuer l’analyse de régression avec l’option Data Analysis
Nous cherchons à obtenir les données de régression multiple. Autrement dit, nous cherchons à comprendre si le nombre d’unités produites, pour chacun des produits a un pouvoir prédictif sur le coût de production total (on peut supposer que oui, mais dans quelle mesure!).
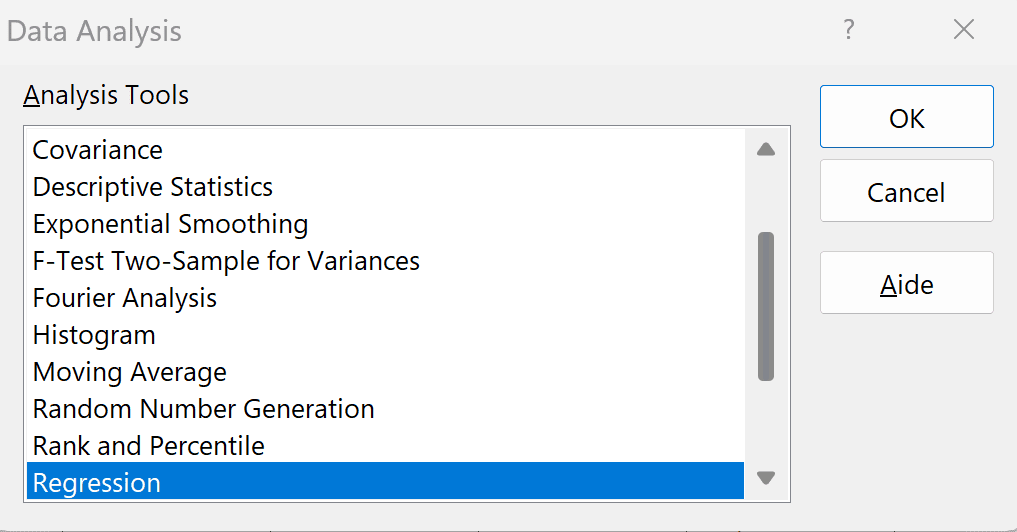
Pour faire l’analyse de régression, nous irons donc dans le menu Données (Data) et nous choisirons le sous-menu Analyse de données (Data Analysis). Ensuite, nous sélectionnerons l’option Régression (Regression) pour effectuer notre régression linéaire multiple.
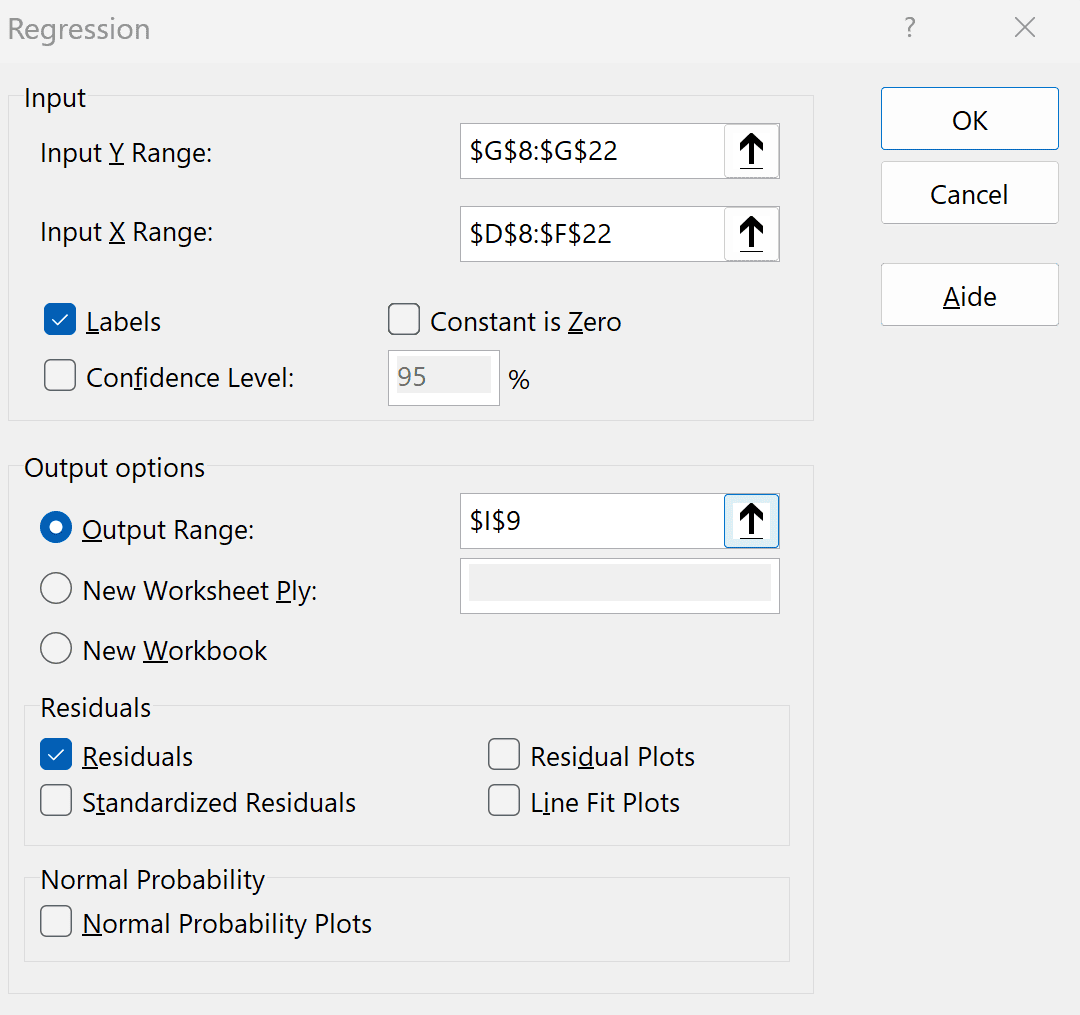
Nous indiquerons à Excel où se trouve notre plage de données Y (les coûts de production) et notre plage de données X (les unités produites pour les 3 produits). Nous lui indiquerons également que nous souhaitons obtenir l’information concernant les résidus. De mon côté, j’ai inclus les entêtes de colonnes dans la plage de données sélectionnées. Je coche donc Labels, ce qui facilitera l’analyse des résultats.
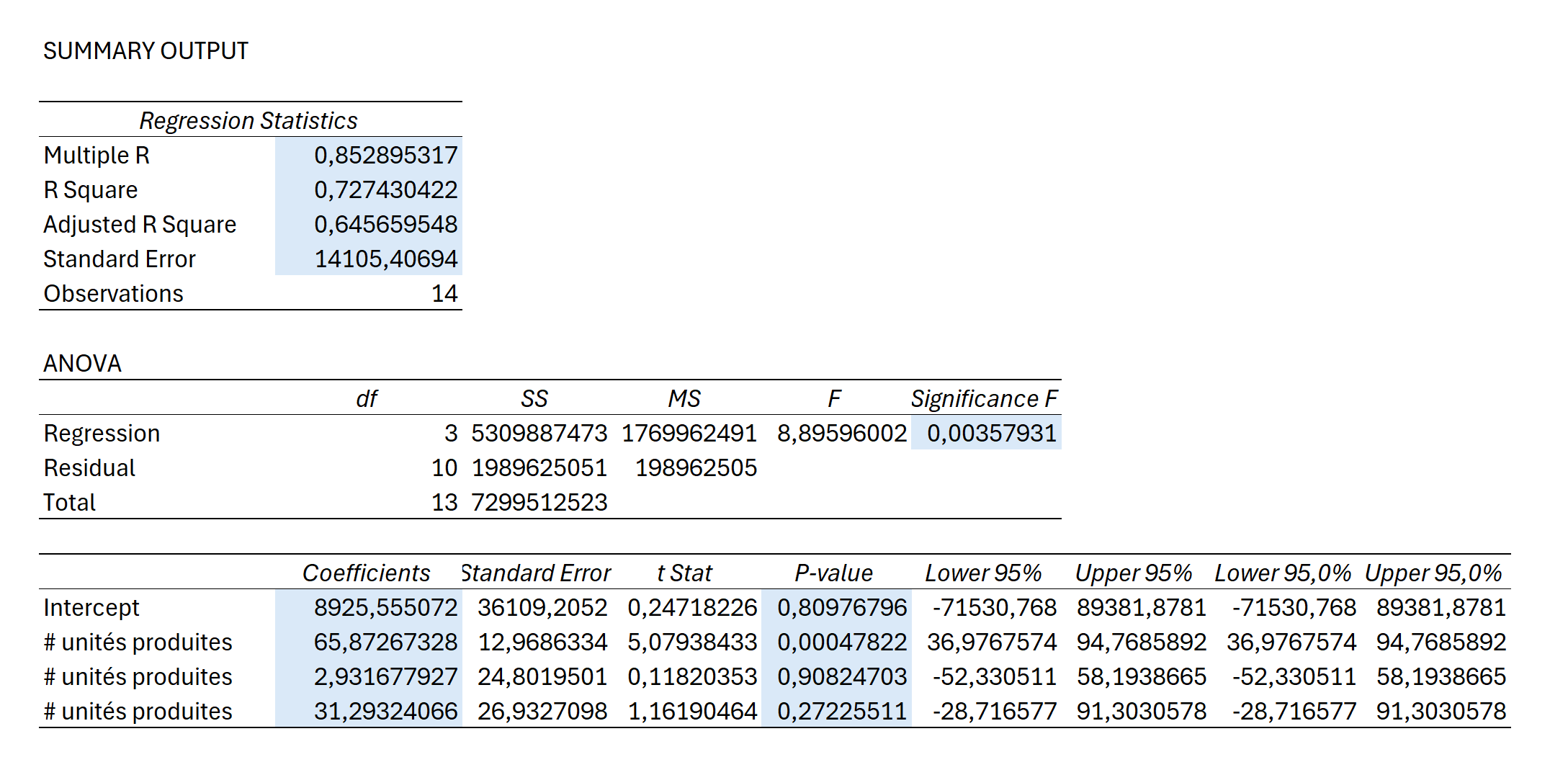
Nous cliquerons ensuite sur OK pour obtenir le résumé suivant, incluant une analyse ANOVA et une analyse de résidus. Porter une attention particulière aux valeurs que nous mises en bleu.
4. Interprétation des résultats
Dans un premier temps, nous devons évaluer la qualité de notre modèle en interprétant les valeurs suivantes :
- Le multiple R indique le degré de corrélation. Une valeur de 0.85 indique une corrélation forte.
- Le R square indique que les 3 variables combinées expliquent 72.7% de la variation du coût de production.
- Le Adjusted R Square, tient compte du nombre de variables et d’observations. Ainsi, en tenant compte de ces deux éléments, le modèle explique 65% de la variation de Y.
- Le Standard Error indique l’écart moyen entre les valeurs réelles et les valeurs prédites. Plus il est faible, plus les prédictions sont précises.
- La Significance F est inférieur à 0.05, ce qui nous indique que le modèle global est statistiquement significatif et nous permet de confirmer qu’au moins une des variables indépendantes contribue réellement à expliquer Y.
Dans un deuxième temps, nous devons évaluer quelles variables sont réellement importantes dans le modèle. La question qu’il faut se poser est : quelles sont les variables qui ont réellement un pouvoir prédictif sur le coût de production. Pour procéder à cette analyse, nous pouvons d’abord observer les “p-value”, qui varie entre 0 et 1. Généralement, un “p-value” égal ou inférieur à 0.05 indique que la variable a un réel pouvoir prédictif. En fait, plus le “p-value” est petit, plus la variable a un potentiel prédictif intéressant.
Dans notre exemple, on peut conclure que la variable 1 (le # d’unités produites pour le produit 1), qui a une p-value de 0.00047822, a réellement un pouvoir prédictif intéressant sur le coût de production alors que les deux autres variables ont un pouvoir prédictif beaucoup moins intéressant. Nous pourrions donc choisir de recommencer notre analyse de régression en utilisant seulement la variable qui a un réel pouvoir explicatif.
5. Construire l’équation
Une fois que nous sommes à l’aise avec le pouvoir prédictif de nos variables explicatives, nous pouvons construire l’équation de la droite à partir des coefficients obtenus.
Ainsi, si nos 3 variables avaient eu un pouvoir explicatif significatif, nous aurions pu estimer avec confiance le coût de production via l’équation suivante :
Y = 8925.55 + 65.8727X₁ + 2,9317X₂ + 31,2932X₃
6. Alternatives
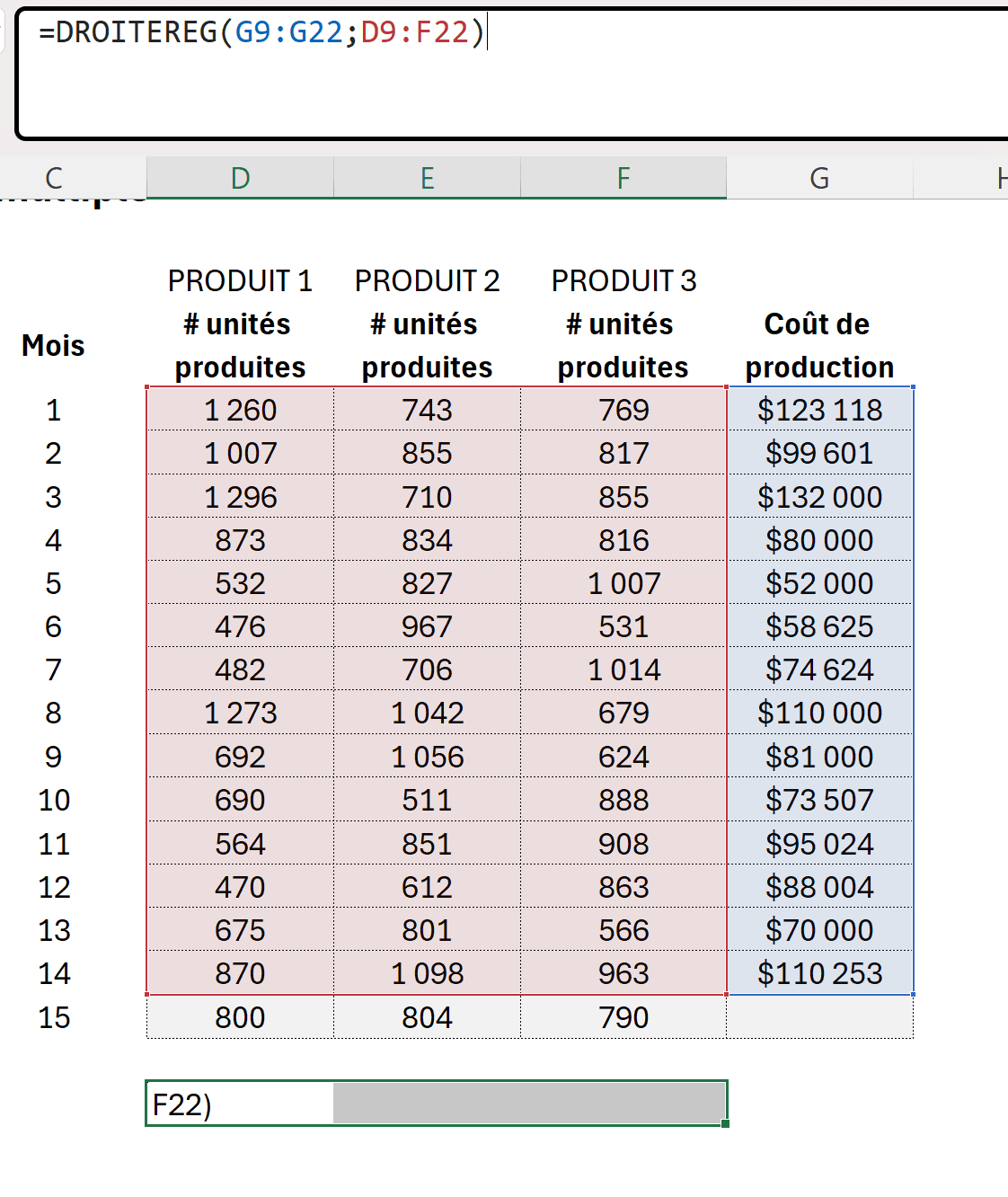
Nous aurions également pu utiliser la fonction DROITEREG (LINEST), tel qu’illustré dans l’article Analyse prédictive dans Excel: Régression linéaire simple. Par contre, puisque nous avons 3 variables explicatives, nous devons d’abord sélectionner 3 cellules de sorties pour notre fonction.
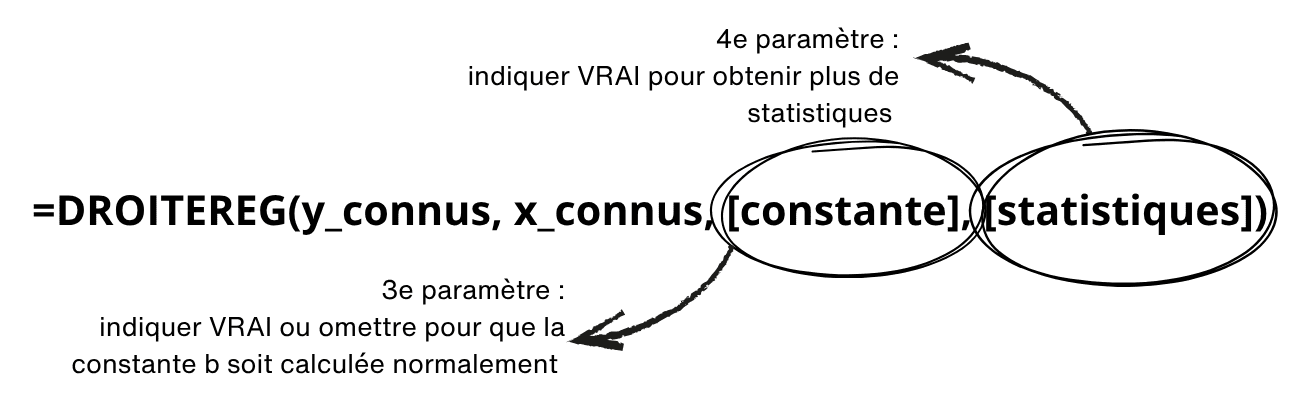
Nous aurions ainsi obtenu l’ordonnée à l’origine et les coefficients de régression directement. Par contre, si nous avions voulu utiliser la fonction DROITEREG et obtenir d’autres statistiques intéressantes telles que celles fournies par la fonctionnalité Data Analysis, il aurait fallu utiliser un paramètre facultatif de la fonction DROITEREG, qui est le 4e paramètre, en indiquant VRAI et en laissant le 3e paramètre vide.
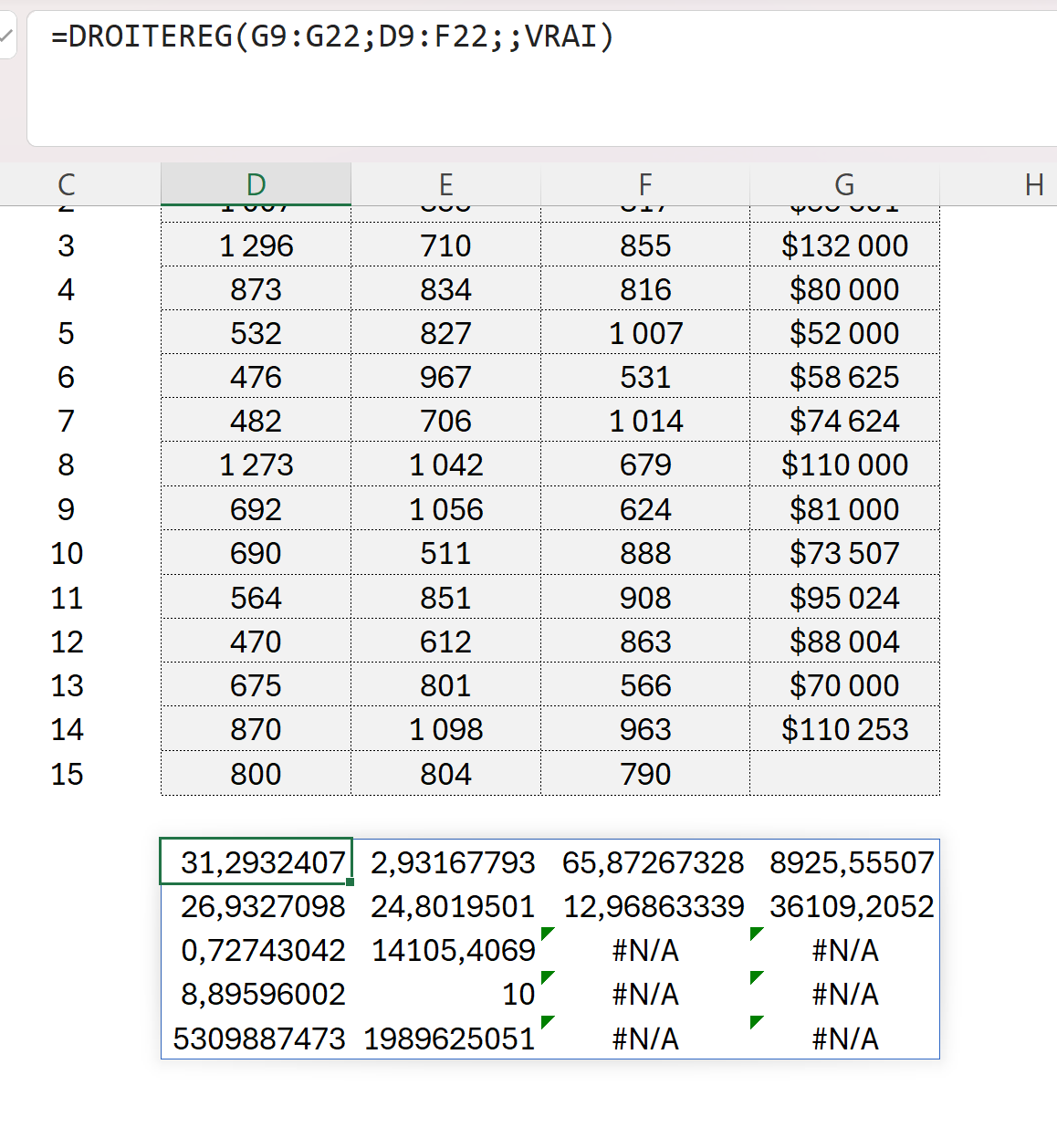
Ainsi, si nous avions écrit notre fonction tel que sur l’image suivante, nous aurions obtenu ceci :
Il est cependant plus difficile d’interpréter le résultat obtenu, car il faut savoir quel chiffre représente quelle statistique, celles-ci n’étant pas identifiée.
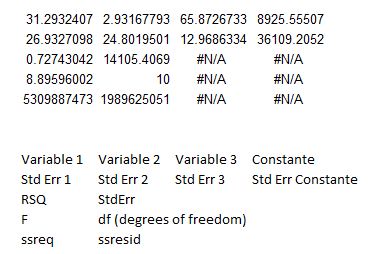
À titre de référence, voici ce que représente chacun des résultats obtenus :
En bref, pour réaliser une analyse de régression simple rapide et efficace, nous vous recommandons d’utiliser la fonction DROITEREG, alors que pour une analyse de régression multiple, la fonctionnalité Data Analysis sera souvent à privilégier puisqu’elle rend plus conviviale l’interprétation de modèles complexes.
Fichier d’accompagnement VIP à télécharger
Pour télécharger le fichier utilisé dans ce tutoriel, devenez membre VIP du CFO masqué.
Formation complémentaire
Afin d’approfondir vos connaissances avec Excel, dont celles touchant à la régression, nous vous recommandons notre formation Excel – Traitement, manipulation et analyse de données).
Voici quelques commentaires d’apprenants ayant suivi cette formation :
La mission du CFO masqué est de développer les compétences techniques des analystes et des contrôleurs de gestion en informatique décisionnelle avec Excel et Power BI et favoriser l’atteinte de leur plein potentiel, en stimulant leur autonomie, leur curiosité, leur raisonnement logique, leur esprit critique et leur créativité.
